Testing an Aurelia SPA

Welcome to the seventh episode about writing an Aurelia SPA. This time we write some unit tests for our custom components.
We also set up E2E testing, something that most of the other Aurelia skeletons come pre packaged with, but that can be a bit messy for a CLI created project.

The “Aurelia SPA built with TypeScript and Sass on .NET Core” Series

These are the parts of this blog post series about building a SPA in Aurelia.

Part I – How to: Build an Aurelia SPA with TypeScript on ASP.NET Core
Part II – How to: Build a Web API on ASP.NET Core for an Aurelia SPA
Part III – How to: Fetching data from a Web API on ASP.NET Core to an Aurelia SPA
Part IV – How to: Creating Aurelia Custom Elements with TypeScript
Part V – How To: Configure and Use the Router in an Aurelia SPA
Part VI – How To: Style an Aurelia SPA with Sass
Part VII – How To: Unit Testing and E2E Testing an Aurelia SPA (CLI)

Aim of This Post

In this post we’ll take a look at testing the code for our Aurelia SPA (built with the Aurelia CLI).
We’ll look at unit testing, have a small word about testing private TypeScript methods. Something that’s missing in the basic CLI project setup, is E2E testing using Protractor, so we’ll set that up as well.

Unit Testing

For this article I rewrote the Network service to use TypeScript’s async/await. I’m going to use that for some unit tests.

There’s also tests where I use the Network service to call a Web Service. That is a mix between a unit and an integration test. I’m using
However it’s useful to see how to handle asynchronous tests.

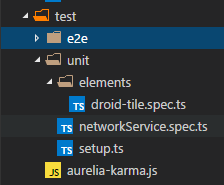
Modifying the File Structure for Unit and End to End Tests

First of I’m going to move around the tests a bit in the folder structure.
Under the tests folder, create a new folder named unit. Under the unit folder I prefer to have folders for each resource type as well, so now I also created a folder named elements.

If you want to setup e2e testing, also create a folder for the end to end tests, name it e2e. Under the e2e folder, create another one named src.

Modifying the Test Setup in the Configuration

To support the new file structure, we need to change the aurelia.json config file.
Modify the unitTestRunner section like this:

  "unitTestRunner": {
    "id": "karma",
    "displayName": "Karma",
    "source": "test\\unit\\**\\*.ts"
  }

To support e2e testing, some more additions is needed to the aurelia.json file, but those will be detailed further down, under the End to End Testing (e2e) section.

Modifying the API CORS Rule for Integration Tests

When doing integration tests and calling the Web API, we need to add Karma’s server address to the CORS rule.

Open up the startup.cs file in the Web API project, and add the address (http://localhost:9876) to the array of approved origins:

   public void ConfigureServices(IServiceCollection services)
        {
            var corsBuilder = new CorsPolicyBuilder();
            corsBuilder.AllowAnyHeader();
            corsBuilder.AllowAnyMethod();
            corsBuilder.WithOrigins("http://localhost:5000", "http://localhost:9876");
            corsBuilder.AllowCredentials();
            services.AddCors(options =>
            {
                options.AddPolicy("AureliaSPA", corsBuilder.Build());
            });

            // Add framework services.
            services.AddMvc();

            //DI
            services.AddSingleton<IDroidRepository, DroidRepository>();
        }

Testing Web Components

Aurelia has a neat component tester that let’s us create our elements in isolation, and then run tests on them. Perfect for unit testing your custom components and making sure they render correct HTML.

Let’s write a test for the droid-tile element we created in a past article, to see how the component tester works.
First I added some new classes to the elements I wanted to test, making locating the elements easier:

<template bindable="droid">
  <div class="tile">
    <div class="row">
      <div class="first">
        <span class="label">ID: </span><span class="value t_id">${droid.id}</span>
      </div>
      <div class="second">
        <span class="label">Name: </span><span class="value t_name">${droid.name}</span>
      </div>
    </div>
    <div>
      <div class="row">
        <div class="first">
          <span class="label">Model: </span><span class="value t_model">${droid.productSeries}</span>
        </div>
        <div class="second">
          <span class="label">Height: </span><span class="value t_height">${droid.height}</span>
        </div>
      </div>
    </div>
  </div>
</template>

See how I added the “t_…” classes to the data bound elements?

The test spec for this element then looks like this:

import { StageComponent } from "aurelia-testing";
import { bootstrap } from 'aurelia-bootstrapper';

describe("droid-tile component test", () => {
    let component;
    const viewModel = {
        droid: {
            id: 55,
            name: "R2-D2",
            productSeries: "R-Series",
            height: 96
        }
    };

    beforeEach(() => {
        component = StageComponent
            .withResources("resources/elements/droid-tile")
            .inView("<droid-tile droid.bind='droid'></droid-tile>")
            .boundTo(viewModel);
    });

    it('should render id', done => {
        component.create(bootstrap).then(() => {
            const element = document.querySelector(".t_id");
            expect(element.innerHTML).toBe(viewModel.droid.id.toString());
            done();
        });
    });

    it("should render name", done => {
        component.create(bootstrap).then(() => {
            const elem = document.querySelector(".t_name");
            expect(elem.innerHTML).toBe(viewModel.droid.name);
            done();
        });
    });

    it("should render product series", done => {
        component.create(bootstrap).then(() => {
            const elem = document.querySelector(".t_model");
            expect(elem.innerHTML).toBe(viewModel.droid.productSeries);
            done();
        });
    });

    it("should render height", done => {
        component.create(bootstrap).then(() => {
            const elem = document.querySelector(".t_height");
            expect(elem.innerHTML).toBe(viewModel.droid.height.toString());
            done();
        });
    });

    afterEach(() => {
        component.dispose();
    })
});

So the, in my opinion ugly, added new classes is only used to find the element for the unit tests.

The alternative is to rely only on the structure of the entire custom element, to find the specific element that is to be tested. And in my opinion, relying on the structure of the element will just lead to a lot of refactoring of the tests. Therefore, as long as your team agrees not to put any kind of styling on the added classes, they are the lesser evil.

At least if the main parameter being considered is development velocity and not code terseness.

Testing Private Methods in TypeScript

Testing private methods is always messy. Often it comes down to special trickery when needing to access private methods. A problem that haven’t been about long for JavaScript, but has been prevalent for a long time for other languages.

As for testing private TypeScript methods you will boil down to either choosing to:

1. Forfeit using private as a scope modifier, to enable access to the methods you need to test
2. Expose the private methods you need to test in some kind of proxy

There is a school that says “you only need to write tests for the API of your classes”, aka the public surface.
But I sometimes prefer to create tests for small private methods as well, at least when they contain tricky logic that I really need to be sure about.

My preference is to create a public object that exposes the private methods that I want to test, and I place it below all other private methods in my files.
In the Network class it looks like this:

    public __test = {
        copyBase: this.copyBase
    }

A simple object, exposing the method that needs to be tested. And we can use it from the test specs like this:

    const network = new Network(undefined);
    const result = network.__test.copyBase(mockResponse as Response);

Adding a Better Karma Reporter

The default Karma test reporter only reports failed tests. But I prefer to see all the tests run, even the passing ones.

Let’s install another reporter, that present us with a little more information about our unit tests:

npm install karma-spec-reporter --save-dev

Then modify karma.conf.js, located in the root of the project.
Change the reporters property to be [‘spec’].

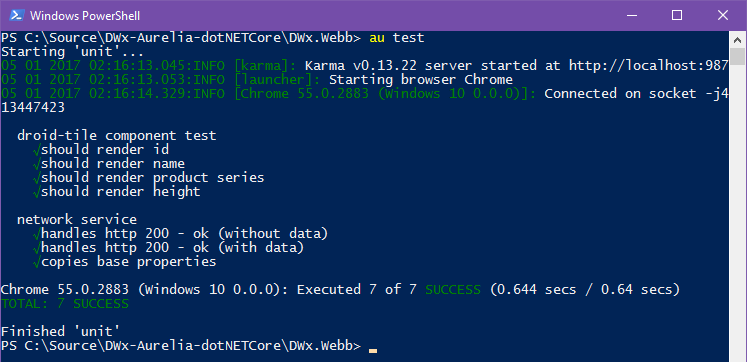
Running the Unit Tests

Start the tests with au test, and add a --watch on the end if you prefer to run them under a watcher.
The result looks something like the following.

End to End Testing (e2e)

A certain amount of code wrangling is required to get E2E testing setup with the CLI. In many of the Aurelia Skeleton apps it’s already setup, but if you like using the CLI there are a few extra steps we need to execute.

What’s needed to get e2e testing running n the CLI project is:

1. Add required dependencies
2. Create protractor.conf.js and aurelia.protractor.js in the root of the project
3. Add e2e.ts and e2e.json in the aurelia_project/tasks
4. Add a e2eTestRunner section in the aurelia_project/aurelia.json file

Add Dependencies

Install the needed dependencies:

npm install --save-dev del
npm install --save-dev gulp-protractor

Add the Protractor Configuration

The Protractor setup needs a config, create a new file and the following code:

exports.config = {
  directConnect: true,

  // Capabilities to be passed to the webdriver instance.
  capabilities: {
    'browserName': 'chrome'
  },

  //seleniumAddress: 'http://0.0.0.0:4444',
  specs: ['test/e2e/dist/*.js'],

  plugins: [{
    path: 'aurelia.protractor.js'
  }],

  // Options to be passed to Jasmine-node.
  jasmineNodeOpts: {
    showColors: true,
    defaultTimeoutInterval: 30000
  }
};

Add the Aurelia Protractor Plugin

Create a new file in the root of the project and add this code:

/* Aurelia Protractor Plugin */
function addValueBindLocator() {
  by.addLocator('valueBind', function (bindingModel, opt_parentElement) {
    var using = opt_parentElement || document;
    var matches = using.querySelectorAll('*[value\\.bind="' + bindingModel +'"]');
    var result;

    if (matches.length === 0) {
      result = null;
    } else if (matches.length === 1) {
      result = matches[0];
    } else {
      result = matches;
    }

    return result;
  });
}

function loadAndWaitForAureliaPage(pageUrl) {
  browser.get(pageUrl);
  return browser.executeAsyncScript(
    'var cb = arguments[arguments.length - 1];' +
    'document.addEventListener("aurelia-composed", function (e) {' +
    '  cb("Aurelia App composed")' +
    '}, false);'
  ).then(function(result){
    console.log(result);
    return result;
  });
}

function waitForRouterComplete() {
  return browser.executeAsyncScript(
    'var cb = arguments[arguments.length - 1];' +
    'document.querySelector("[aurelia-app]")' +
    '.aurelia.subscribeOnce("router:navigation:complete", function() {' +
    '  cb(true)' +
    '});'
  ).then(function(result){
    return result;
  });
}

/* Plugin hooks */
exports.setup = function(config) {
  // Ignore the default Angular synchronization helpers
  browser.ignoreSynchronization = true;

  // add the aurelia specific valueBind locator
  addValueBindLocator();

  // attach a new way to browser.get a page and wait for Aurelia to complete loading
  browser.loadAndWaitForAureliaPage = loadAndWaitForAureliaPage;

  // wait for router navigations to complete
  browser.waitForRouterComplete = waitForRouterComplete;
};

exports.teardown = function(config) {};
exports.postResults = function(config) {};

Add the E2E Task

Create a new task by adding these files to the aurelia_project/tasks folder:

{
  "name": "e2e",
  "description": "Runs all e2e tests and reports the results.",
  "flags": []
}

/**
 * e2e task
 * 
 * You should have the server up and running before executing this task. e.g. run `au run`, otherwise the
 * protractor calls will fail.
 */
import * as project from '../aurelia.json';
import * as gulp from 'gulp';
import * as del from 'del';
import * as typescript from 'gulp-typescript';
import * as tsConfig from '../../tsconfig.json';
import {CLIOptions} from 'aurelia-cli';

import { webdriver_update, protractor } from 'gulp-protractor';

function clean() {
  return del(project.e2eTestRunner.dist + '*');
}

function build() {
  var typescriptCompiler = typescriptCompiler || null;
  if ( !typescriptCompiler ) {
    delete tsConfig.compilerOptions.lib;
    typescriptCompiler = typescript.createProject(Object.assign({}, tsConfig.compilerOptions, {
      // Add any special overrides for the compiler here
      module: 'commonjs'
    }));
    
  }

  return gulp.src(project.e2eTestRunner.typingsSource.concat(project.e2eTestRunner.source))
    .pipe(typescript(typescriptCompiler))
    .pipe(gulp.dest(project.e2eTestRunner.dist));
}

// runs build-e2e task
// then runs end to end tasks
// using Protractor: http://angular.github.io/protractor/
function e2e() {

  return gulp.src(project.e2eTestRunner.dist + '**/*.js')
    .pipe(protractor({
      configFile: 'protractor.conf.js',
      args: ['--baseUrl', 'http://127.0.0.1:9000']
    }))
    .on('end', function() { process.exit(); })
    .on('error', function(e) { throw e; });
}

export default gulp.series(
  webdriver_update,
  clean,
  build,
  e2e
);

Add a e2eTestRunner section to aurelia.json

Add a new section to the aurelia.json file.

  "e2eTestRunner": {
    "id": "protractor",
    "displayName": "Protractor",
    "source": "test/e2e/src/**/*.ts",
    "dist": "test/e2e/dist/",
    "typingsSource": [
      "typings/**/*.d.ts",
      "custom_typings/**/*.d.ts"
    ]
  }

Write a E2E Test Spec

Write a spec and put it under tests/e2e/src.

This is a sample spec that loads the Home page and checks the browser title and verifies that it has the correct name. The second test executes a click on the navigation element, waits for the browser to navigate, then checks the browser title and makes sure it has navigated.

describe('DroidWorx', () => {
    beforeEach(() => {
        browser.loadAndWaitForAureliaPage('http://localhost:5000');
    });

    it('should show the home page', () => {
        const title = browser.getTitle();
        expect(title).toEqual('Home | Droid Worx');
    });

    it('should navigate to droids list', () => {
        const nav = element(by.id('#/droids')).click();
        browser.waitForRouterComplete();

        const title = browser.getTitle();
        expect(title).toEqual('Droids | Droid Worx');
    });
});

I modified the navigation elements and added an id to them, to enable finding them easier from the test spec.
The page-header element now looks like this:

<template bindable="router">
  <div class="header">
    <h1>${router.title}</h1>
    <nav>
      <ul>
        <li repeat.for="row of router.navigation">
          <a href.bind="row.href" id.bind="row.href">${row.title}</a>
        </li>
      </ul>
    </nav>
  </div>
</template>

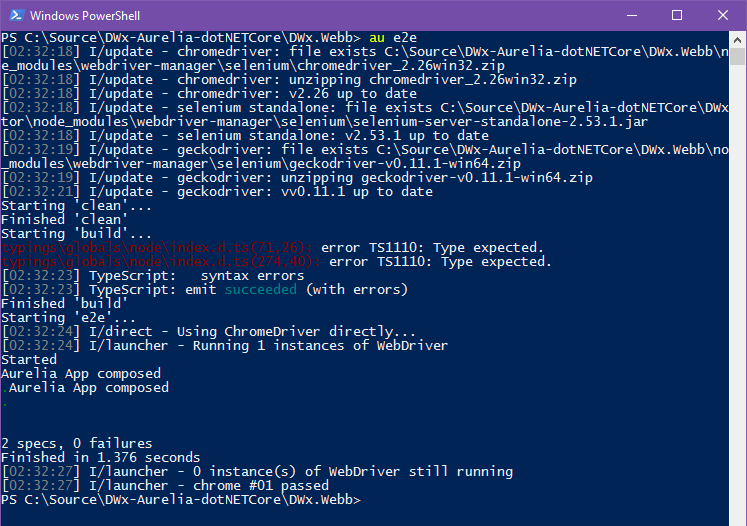
Running the E2E Tests

Run the tests by entering the following in your favorite cmd prompt:

au  e2e

During the execution you will see a browser start, and might even see the Aurelia SPA we built flicker for a bit:)
The result:

Conclusion

Setting up testing is one thing, but in my opinion, the hardest part about testing is actually writing good tests. The tests in this post was very simple, but hopefully proved to be a quick way to get started for you.

Get the Code

The code for this blog series is available on my GitHub repo, you can find it here: DWx-Aurelia-dotNETCore

Until next time,
Happy Coding! 🙂